[cs231n-lec3] Loss Functions and Optimization

최종 수정일 : 2019-10-17

이 포스트는 스탠포드의 cs231n 3강 강의를 보고 공부 및 정리한 포스트입니다.
잘못된 것이 있을 수 있습니다.
댓글로 알려주시면 감사합니다!

Loss Functions and Optimization

지난 강의를 정리한 포스트(lec2)에서는 $f(x, W)=Wx$ 를 이용해 $W$의 값을 구해본다고 했다.
아래의 예시를 보자.

이러한 $W$ 를 얻었다고 했을 때, loss function 으로 무엇을 할 수 있을까?

Loss Functions

바로 우리의 classifier 가 얼마나 잘 분류하는지 알려주는 척도가 될 수 있다.
우리는 지금 분류기를 만들고 있고, 이 분류기의 성능을 높이려 한다. 이 때 loss function 을 이용해 분류기를 평가하고 방향을 생각해 볼 수 있는 것이다.

loss 는 data 들에 대한 개별 loss 의 평균으로 계산할 수 있으며, 이를 수식으로 표현하면 다음과 같다.

$L = {1 \over N} \sum_iL_i\left(f\left(x_i, W\right),y_i\right)$

우리는 두 개를 분류할 수도 있지만(0, 1) 더 많은 클래스를 분류할 경우가 훨씬 많다.
이를 위해 Multiclass SVM loss 을 사용할 수 있는데, 개별 loss $L_i$ 는 다음과 같다.
$\begin{aligned} L_i &= \sum_{j \ne y_i}\begin{cases}0 & \text{if } s_{y_i} \geq s_j + 1 \ s_j - s_{y_i} + 1 & \text{otherwise } \end{cases} \ &= \sum_{j \ne y_i } max(0, s_j - s_{y_i} + 1) \end{aligned}$

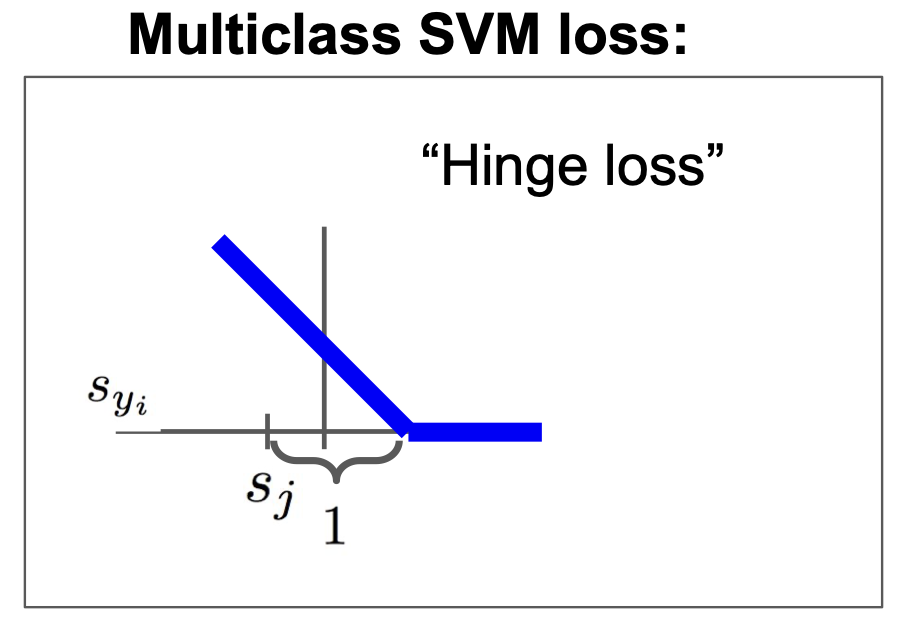
이는 Hinge Loss 라고도 불린다.(경첩..?)

위의 식 $L_i = \sum_{j \ne y_i } max(0, s_j - s_{y_i} + 1)$ 을 이용해 $L_i$ 를 구해보면 각각 2.9, 0, 12.9 가 된다.
이를 평균 낸 것이 $L$ 이 되므로, L = 5.27 이 된다.
나중에 자세하게 보게 되겠지만, loss L 이 작아지는 방향으로 설계를 해야 제대로 된 학습이 이루어지는 것을 의미하게 된다.

여기서 몇 가지 질문을 생각해 볼 수 있는데,

1. car 의 score 가 조금 변화하면 loss 에는 어떤 변화가 있을지?
2. loss 의 최대/최소 는?
3. 초기에 W 와 그 때의 loss 는?
4. $j = y_i$ 를 포함했을 때 loss 는?
5. 합 대신 평균값을 이용하게 된다면 어떤 차이를 가지고 오는가?
6. $L_i = \sum_{j \ne y_i } max(0, s_j - s_{y_i} + 1)^2$ 을 사용하면 어떻게 되는가?

등등이 있다. 각각의 답은 어떨까?

1. loss 변화는 없다. Multiclass SVM loss 에서는 오직 정확한 score 를 잘못된 score보다 1만큼 더 크도록 하는 과정이고, 이미 car score 는 다른 score 들에 비해 충분히 크므로 car score 가 조금 변화한다고 해서 loss 에 차이가 발생하지는 않는다.(이미 0의 구간에 위치)
2. min = 0, max = $\infty$ (그래프 참조)
3. class의 개수 N보다 1만큼 작은 N-1이 된다. 초기 W 는 모두 0이고, 이에 따라 $L_i$ 는 각각 N-1 이 될 것이다. loss 는 결국 N-1 이 된다.
4. 이는 $L_i$ 가 각각 1씩 증가하게 되는 것으로, 결국 loss 도 1 증가하게 된다.
5. 딱히 변화는 없다. 우리는 true value 또는 true loss 를 찾기를 원하고 그 과정 속에서 scale 하는 방법의 차이가 있을 뿐 결과적으로는 같은 방향으로 나아가게 되기 때문이다.
6. 차이가 생긴다. Hinge loss 에서는 1차, 즉 linear 한 부분이 있는데, 이는 2차의 부분이 생기게 되고(squared) 이러한 nonlinear 함은 다른 loss function 이 되게 된다.

또 다른 질문도 있다.

$f(x, W) = Wx$
$L = {1 \over N} \sum_{i=1}^N \sum_{j \ne y_i} max\left(0, f\left(x_i;W\right)j - f\left(x_i;W\right){y_i} + 1 \right)$
이러한 W 와 L 에 대해서 $L=0$ 이 되는 $W$ 를 찾았을 때, $W$ 는 유일한가? 라는 질문이다.

물론 $W$ 는 유일하지 않은데, $2W$ 에 대해 생각해보자.

0이 된다는 것은 max 부분에서 0와 음수가 비교된 것이고, 이는 이미 correct score 와 incorrect score 의 차이가 1보다 크다는 의미이다. 이 때 2배를 해주면 여전히 그 차이는 1보다 크기 때문에 여전히 0 이 나오게된다.

우리는 이제 위의 질문들에 대해 유념하며 $W$ 를 어떻게 잘 구할 것인가를 생각해보아야 한다.

위의 문제가 발생한 이유는 우리가 classifier 에게 training data 에 대해 $W$ 를 맞추라는 이야기만 하고 있기 때문이다.
그러나 현실에서는 꼭 training data 에 대해 맞는 $W$ 를 구할 필요는 없다.
이는 Machine Learning 의 관점에서 보면, 우리는 결국 training data 로 만들어 낸 모델을 test data 에 적용시켜서 문제를 해결하려는 것이기에 사실 training data 에서의 성능보다는 test data 에서의 성능이 훨씬 더 중요하기 때문이다. 그리고 이 test data 는 training data 와는 다를 수 있다.
즉, test data 에서의 성능을 위해 training data에 완벽히 맞추지 않고 적당히 맞추는 과정이 필요한데, 이것이 바로 Regularization 이다.

---

Regularization

우리는 지금까지 다음과 같은 loss function 에 대해 살펴보았다.

$L(W) = {1 \over N} \sum_{i=1}^N L_i\left( f \left( x_i, W \right), y_i \right)$

이제 Regularization 을 적용해서 수식을 보자.

$L(W) = {1 \over N} \sum_{i=1}^N L_i\left( f \left( x_i, W \right), y_i \right) + \lambda R \left( W \right)$

우변의 첫 번째 항이 data loss 가 되고, 두 번째 항이 regularization 이 된다.
data loss 는 모델이 training data 에 대해 학습할 수 있도록 해주며, regularization 은 모델이 너무 training data 에 매몰되지 않도록 해주는 역할이다.

여기서 $\lambda$ 는 hyperparameter 로, 적합한 값을 선택해 주어야 한다.

regularization 을 하는 방법은 다양한데, 간단하게 L1, L2 regularization 이 있으며, 이 둘을 같이 사용하는 Elastic net 도 있다.

L2 : $R(W) = \sum_k \sum_l W_{k,l}^2$
L1 : $R(W) = \sum_k \sum_l \left| W_{k,l} \right|$
Elastic net : $R(W) = \sum_k \sum_l \beta W_{k,l}^2 + \left| W_{k,l} \right|$

그 외에도 dropout, batch normalization, stochastic depth, fractional pooling 등이 있다.

정규화를 하는 이유는 다음과 같다.

1. 가중치에 대한 선호도를 표현(express preferences)
2. 모델을 simple 하게 만들어 test data 에서 사용
3. 곡률을 추가하므로써 최적화 향상

(1) 에 대해 조금 살펴보자.

$x = \left[ 1,1,1,1 \right]$
$w_1 = \left[ 1,0,0,0 \right]$
$w_2 = \left[ 0.25,0.25,0.25,0.25 \right]$

로 주어졌을 때,

$w_1^Tx = w_2^T = 1$ 이지만, L2 regularization 은 $w_2$ 를 더 선호한다.
이는 가중치가 더 고루 퍼져있기 때문이다. 그러나 이는 항상 고정적이지는 않고 경우에 따라 다를 수 있다.

(2) 는 아래의 그림을 보면 이해가 쉽다.

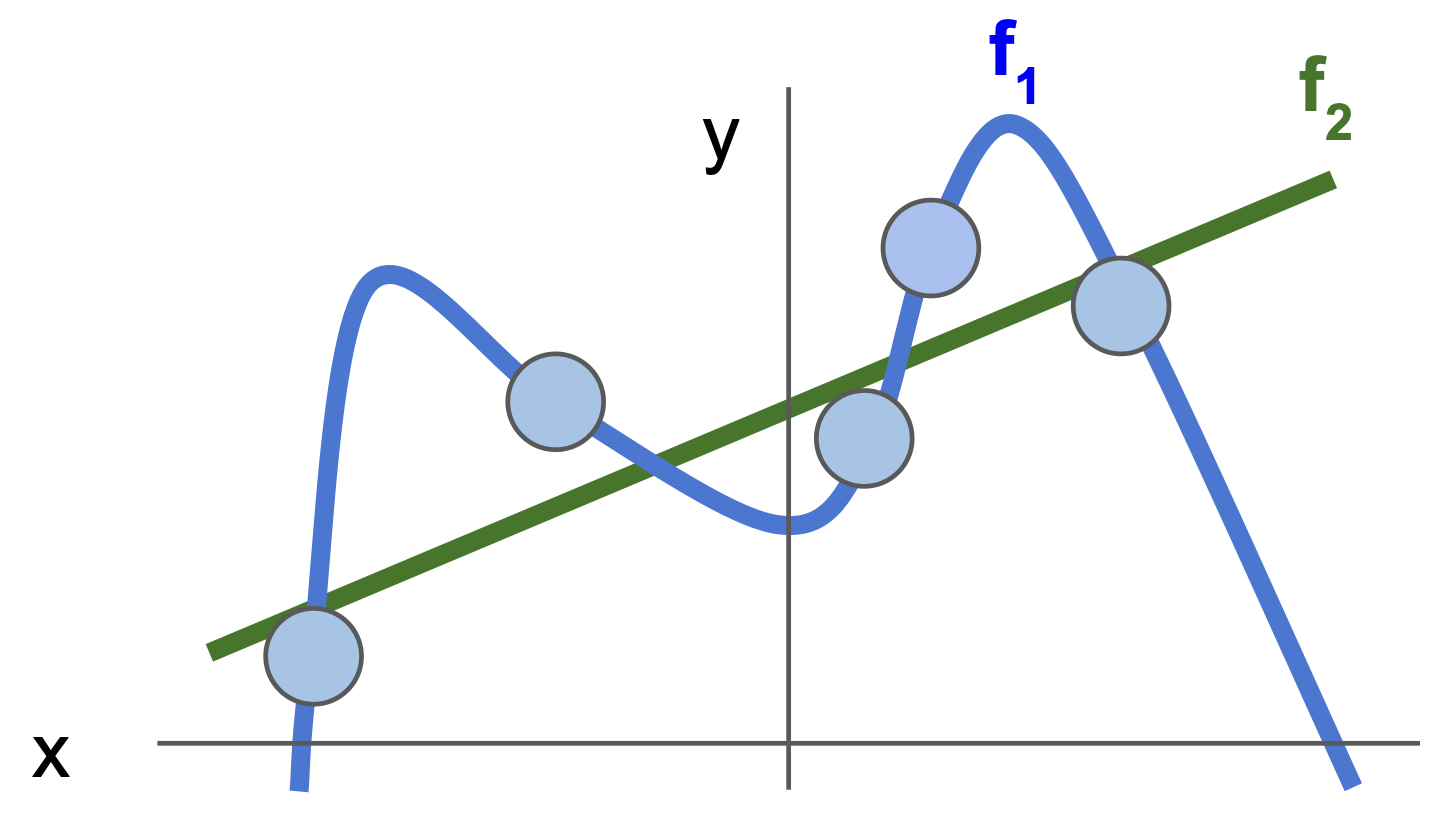
f1은 training data 에 많이 fit 시켜놓은 것이고 f2 는 느슨하게 fit 시켜놓은 상태이다.
여기서 test data 가 아래의 회색처럼 들어오게 된다면,

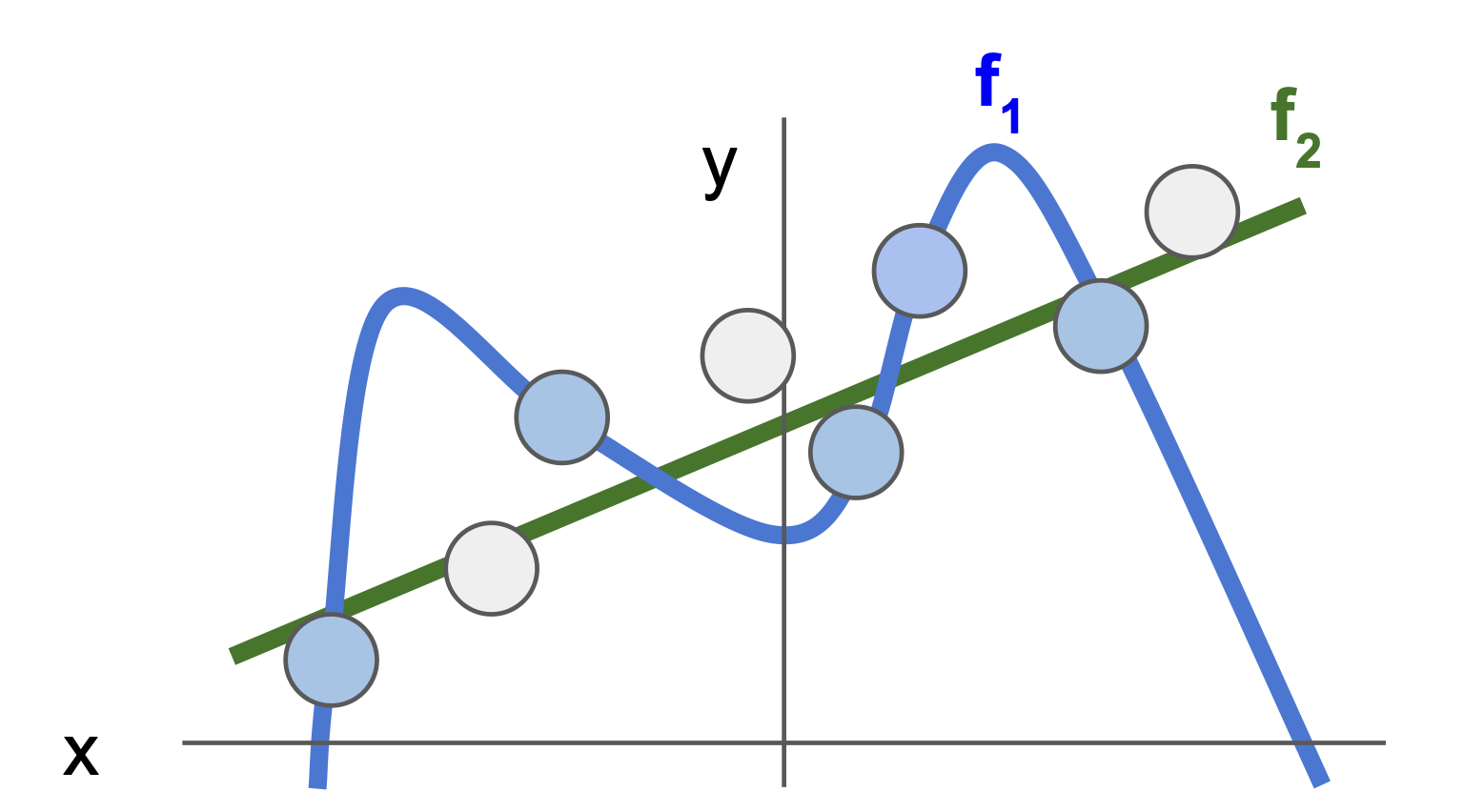
f1과 f2 각각의 test data 와 gap 을 비교해보면 f2 가 더 test data 에 근접함을 볼 수 있다.

이처럼 정규화를 통해 모델을 더 simple 하게 만들면 test data 에서 더 좋은 성능을 얻을 수 있으며, 현실의 문제에서도 이러한 접근법이 타당하다는 것이 실증적으로 나타나있다.

---

Softmax Classifier

이제 softmax 에 대해 알아보자.
softmax 는 입력받은 값을 출력으로 할 때 0~1 사이의 값을 가지며, 그 총합이 1이 되도록 하는 함수이다.
수식은 다음과 같다.

$P \left(Y = k

X = x_i \right) = { e^{s_k} \over \sum_j e^{s_j} }$

그리고 이에 따른 loss $L_i$ 는 다음과 같다.

$L_i = -\log P \left(Y = y_i

X = x_i \right)$

위의 내용들을 정리해 보면,

여기서 $L_i$ 는 cross-entropy loss 라고도 불린다.

앞서 SVM loss 를 했을 때 했던 질문처럼 여기서도 비슷한 질문을 던질 수 있는데,

1. loss 의 최대/최소는?
2. 초기의 loss 값은?

마찬가지로 생각해서 답을 해 볼 수 있다.

1. min = 0, max = $\infty$
2. log(C), 여기서 C는 클래스의 개수이다.

여기서 loss 의 값이 0~$\infty$ 값을 가지게 되는데 이것은 좋지 못한 것이다.
그러나 실제적으로는 양 극단의 값을 갖기 매우 어렵기에 현실적으로 그러한 문제가 발생하기는 드물다.(0이 나오려면 correct score 가 정확히 모두 맞는 경우(=1)여야 하는데(이 때, -log 1 이 되서 loss=0), 이러한 경우가 드물기 때문. $\infty$ 도 같은 맥락에서 볼 수 있다.(완전히 틀린 경우, correct score = 0)). 이 때 확률분포에 따라 모두 맞는 것이라면 $\infty$ 의 값이 필요하고, 마찬가지로 모두 틀리려면 $-\infty$ 의 값이 필요하게 된다. 컴퓨터는 이러한 무한과 관련한 연산을 하기 힘들기에 우리가 실제적으로 이렇게 양 극단의 loss 값을 갖는 것은 어렵다.

초기의 loss 값을 생각하고 넘어가는 이유는 뭘까? 바로 sanity check 를 할 수 있기 때문인데, debugging 시 초기화를 한 후 실제로 저 값이 나오는 지를 테스트해서 만약 다른 값이 나온다면 코드에 문제가 있음 알 수 있다.

SVM loss 와 softmax 의 차이가 무엇이 있을까?

간략하게 생각하면 SVM loss 는 correct score 와 incorrect score 의 차이에 대해 본다면, softmax 는 correct score 가 점수가 높고, incorrect score 가 점수가 낮을 경우, 이것을 더욱 모아서 correct score 는 +$\infty$로 보내려하고, incorrect score 는 -$\infty$ 로 보내려하는 차이가 있다!

---

여기까지 loss 와 loss function 그리고 regularization 까지 간략하게 살펴보았다.
우리의 목표는 좋은 $W$ 를 찾아 loss 를 최소화하고 싶은 것인데, 그렇다면 이 좋은 $W$ 는 어떻게 찾을 수 있을까?

Optimization

들어가기에 앞서, 다음의 예시를 생각해보자.

당신은 지금 산 속 어딘가에 위치해있다. 현재 당신의 목표는 산에서 내려가는 것이다. 어떻게 내려갈 것인가?

위의 질문은 현실 속의 문제를 아주 간략하고 추상화한 문제이다.
우리가 앞서 살펴보았던 loss 와 W 의 최적화된 값을 구할 때, 정말 고도의 분석력을 이용해 한 번에 답(minimizer)을 적어내려갈 수 있을까?

이는 위 질문에서 이렇게 답하는 것과 같다.

나는 산 중턱 어딘가에 있는데, 순간이동을 통해 산 아래로 내려가는 거야.

순간이동이라니! 솔직히 이는 말이 안된다. 조금 더 현실적으로 산에서 내려올 방법을 강구해보자.

방향을 정확하게 모른다면 이 곳이나 저 곳이나 가 볼 수 밖에 없겠지

이러한 방법이 바로 random search 가 되겠다. 산에서 눈을 가리고 그냥 돌아다니다가 얻어 걸리라는 식의 방법이다. 이런 식으로 산에서 내려와 볼 때, 무사히 내려올 수 있을 확률이 얼마나 될까?

15.5% 이다. 이 정도면 막무가내로 그냥 한 것 치고는 나쁘지 않지 않은가?
이 수치는 실제로 random search 를 CIFAR-10 에 적용했을 때 나오는 수치이다. 그러나 가장 좋은 성능을 내는 모델의 경우 무려 95%의 성능이 나온다!

그렇다면 좀 더 현실적으로 생각해보자.
현재 시점에서 아래로 가는 방향을 찾아서 그 방향으로 간다면 산 아래로 끝까지 갈 수 있지 않을까? 어쨌든 우리는 아래로 가는 것이 목표였으니까!

Gradient Descent

이렇게 해서 만들어 낸 방법이 바로 경사하강법(Gradient Descent)이다.

미적분학 시간에 배운 순간기울기를 잠시 생각해보자.

${ df\left(x \right) \over dx} = \lim_{h \to 0}{f\left(x + h \right) - f \left( x \right) \over h}$

이를 이용해서 현재의 $W$ 에서 아주 조금씩 바꿨을 때의 변화(순간기울기)를 구해 볼 수 있다.
아래는 그 과정이다.

그러나 이렇게 하나씩 gradient 를 구하는 것은 너무 느린 작업이다. 우리는 이미 미분을 할 수 있지 않은가?
즉, $\nabla_W L$을 구하면 그만이다. 이를 analytic gradient 라고 한다.위의 방식으로 구하는 것은 numeric gradient

numeric gradient 는 마찬가지로 gradient check(진짜 잘 계산 되는지) 에서나 쓰고 analytic gradient 로 빠르게 계산해보자.

Gradient Descent는 다음과 같이 코드로 작성될 수 있다.

# Vanilla Gradient Descent

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # perform parameter update

여기서 step_size 는 한 번에 얼만큼 그 방향으로 진행할 지를 의미하는데, 이는 hyperparameter 이다. learning rate 라고도 불리는 이 hyperparameter 는 아주 중요한 것으로써 학습 시 매우 신중하게 설정해야 좋은 성능을 가진 모델을 학습시킬 수 있다.

또한 weight 에 - 로 업데이트 하는 이유는 gradient 가 그 방향의 최대가 되는 값이고 우리가 구하려는 것은 최소(내려간다!)이기 때문에 반대 방향으로 값을 주어야 한다.

이렇게 step_size 와 gradient 로 학습을 시키게 되는데, 다양한 update rule 에 대해 천천히 학습해보도록 하자.

그 전에 Stochastic Gradient Descent(SGD) 에 대해 간단하게 살펴보자.

loss 를 구할 때 우리는 전체 N 에 대해 값을 계산해주었다.
만약 N 이 아주 큰 숫자라면? loss 를 한 번 구하는데 굉장히 오래 걸리게 될 것이다.
이러한 문제를 피하기 위해 우리는 표본(minibatch, 보통 2의 제곱 크기(32, 64, 128, …))을 추출해 loss 를 구하고 이것을 전체 데이터셋이라고 가정한 뒤 업데이트를 진행하는 방식을 생각할 수 있다.

Image Feature

이미지를 분류하는 고전적인 방법에 대해서 간단하게 봐보자.

image 에서 feature를 추출해 낸 다음에 여기에 linear classification 을 적용했었다.

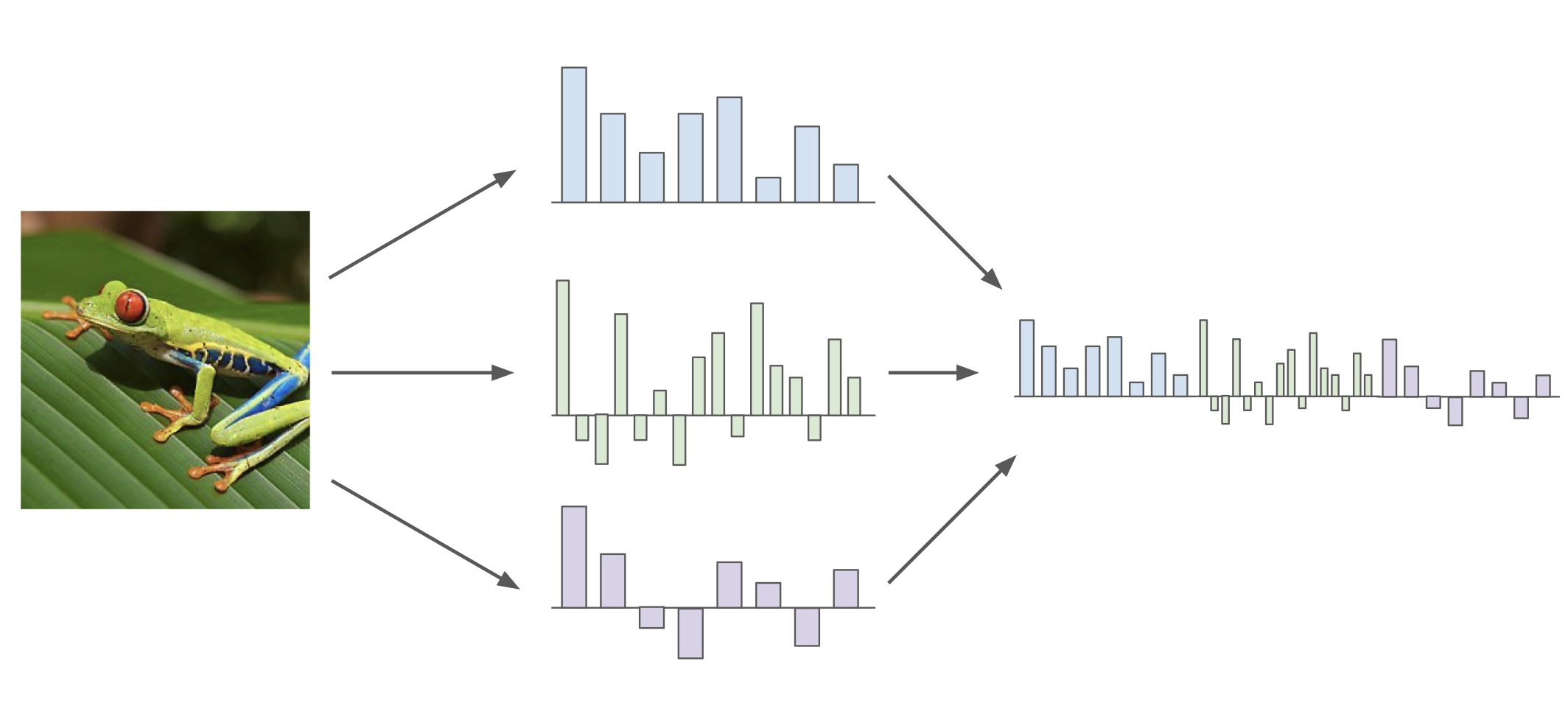
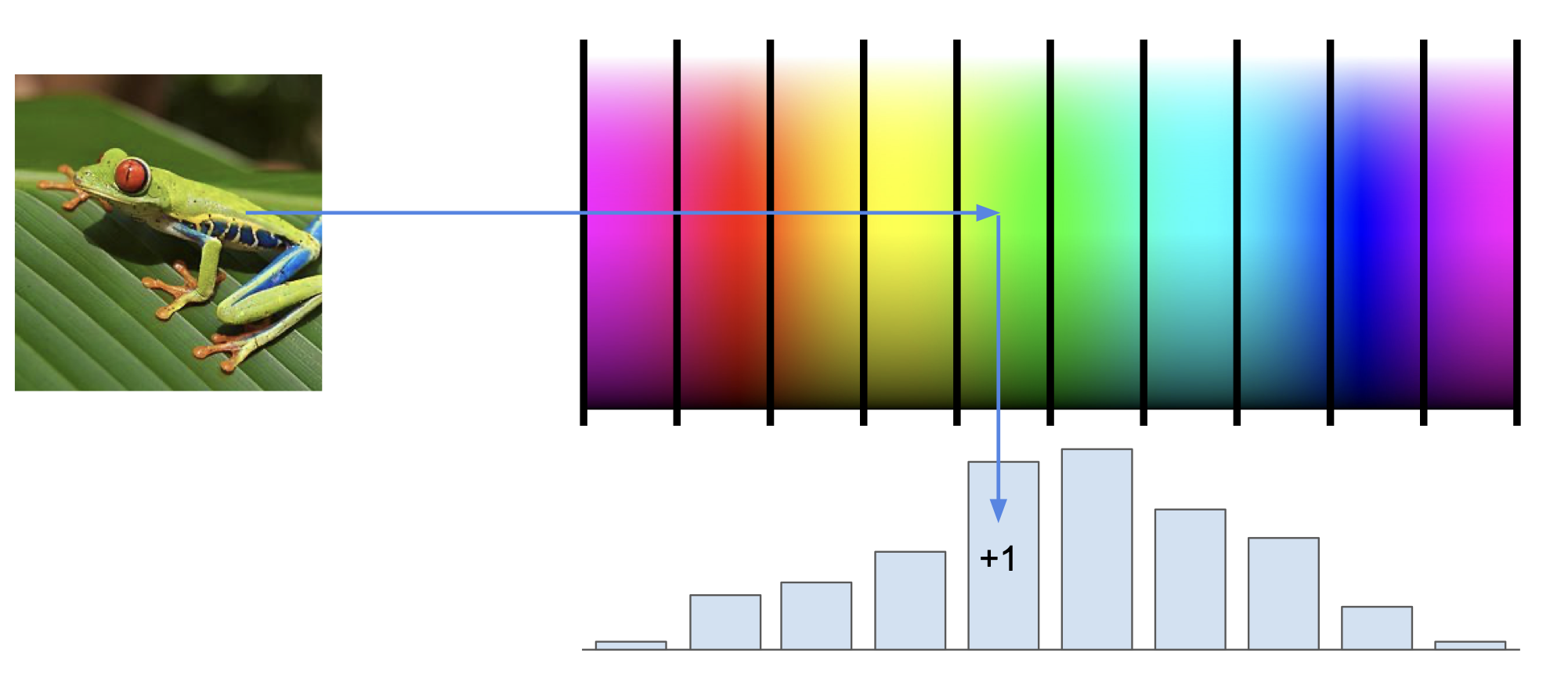
color histogram

여러 feature 들을 추출한 다음에 이를 concatenation(붙이기) 시켜서 이어 붙인 후 적용시키는게 일반적이었는데, feature 를 추출하는 대표적인 방법으로는 color histogram 이 있다.

이는 픽셀이 나타내는 색상에 해당하는 값을 +1 증가하여 histogram 으로 표현하는 방법이다.

histogram of oriented gradient

이미지에서 8*8 픽셀의 edge 에 대해 아홉 가지 방향에 대한 값을 바탕으로 feature 를 추출하는 방식도 있다.

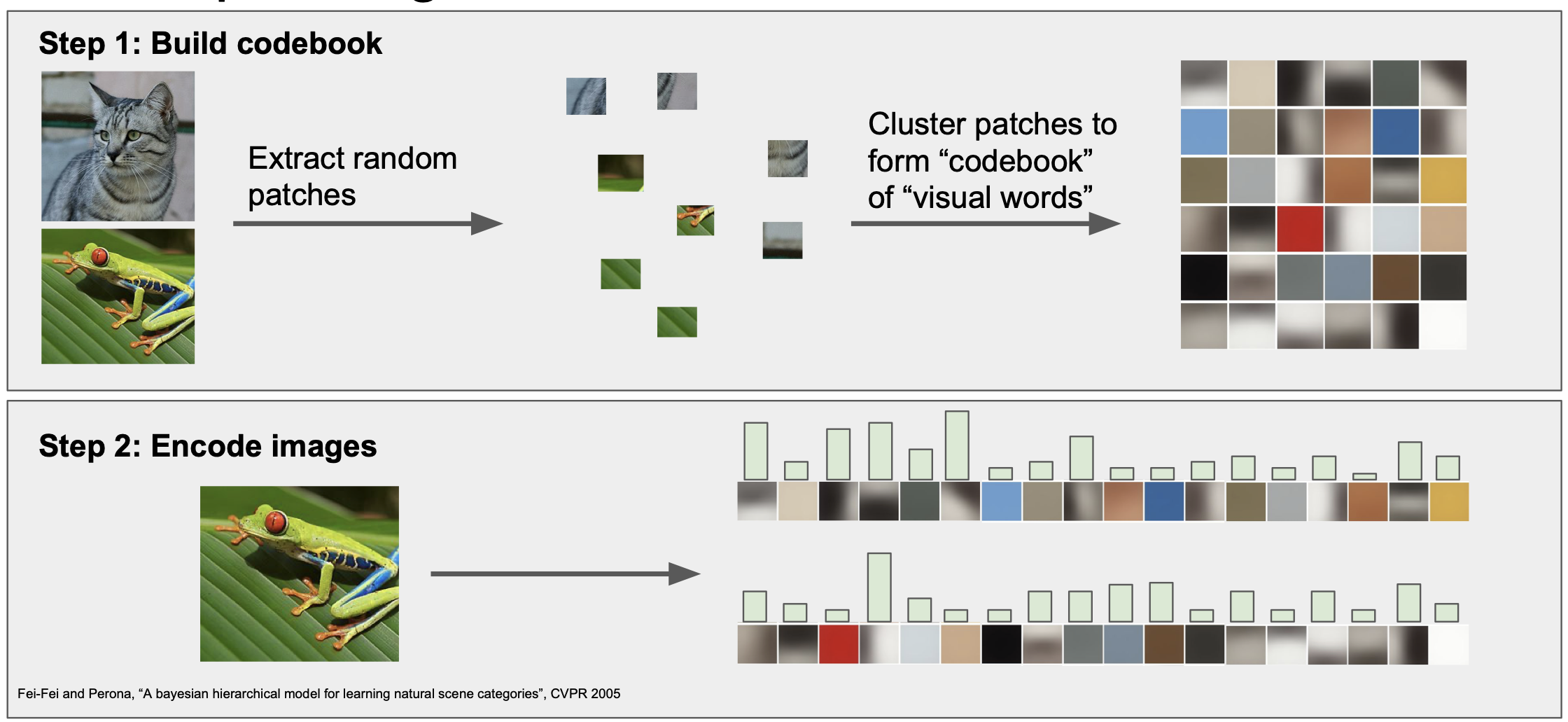
bag of words

또는 임의의 patch 로 이미지들을 분리한 다음 codebook 의 형태로 이미지에 대한 모임을 만들어 놓은 뒤 해당 하는 이미지에 대한 대응 값을 토대로 histogram 을 만드는 기법도 있다.

---

전통적인 방법을 아주 간단히 살펴보고 image feature 를 어떻게 추출해서 학습하는지 간략하게 생각해보았다.

다음에는 이러한 전통적인 방법과 현대의 ConvNet 의 차이점에 대해서 알아볼 것이다.

간단하게 요약하면 다음과 같다.

전통적인 방법으로는 image feature 를 찾아내 이를 이용한 분류 작업을 진행했다면,
ConvNet 에서는 찾아내는 것 없이 스스로 parameter 를 학습해서 분류 작업을 진행하게 된다.