Digital Signature

정보보호에서 Digital Signature 란 무엇인지 간략히 학습해보자.

Digital Signatures

앞서 우리는 Message Authentication 에 대해서 살펴봤다.

이를 통해 두 파티 간의 메세지 교환을 third party(공격자)로부터 보호할 수 있긴 하지만 서로 보호할 수는 없는 방식(신뢰할 수 있는 통신의 문제)이다.

이런 문제점을 해결하기 위해 Digital Signature 를 도입하게 되었다.
이를 통해 우리는 다음이 가능해진다.

• author, date, time 을 verify 할 수 있다.
• message contents 를 authenticate 할 수 있다.
• 분쟁을 해결하기 위해 third party 가 확인 가능하다.

그러나 이는 unique verification 으로는 불가능하며, authentication function 에 또 다른 것들을 추가하므로써 가능케한다.

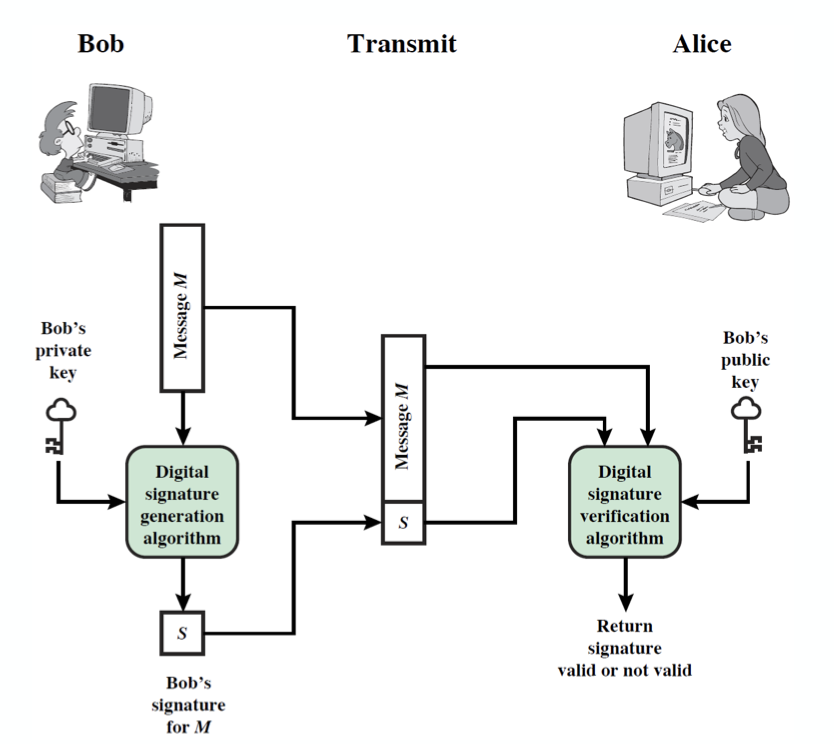
Digital Signature 의 모델은 위와 같다.

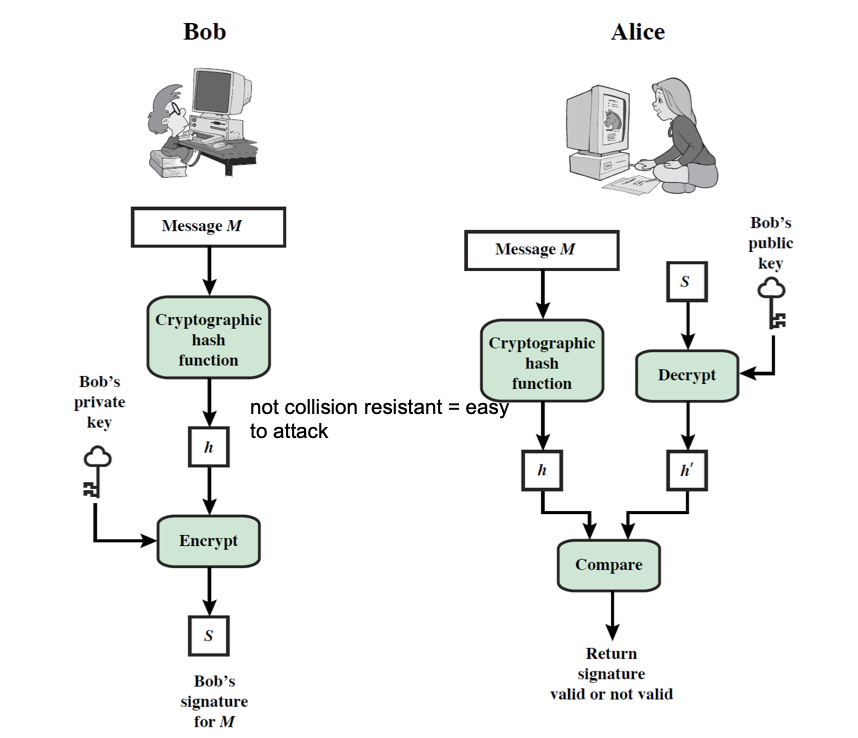
이 때 필요한 elements 들이 위에 나타나있다.

• Cryptographic hash function
  • 이는 collision resistant 해야 한다. 그렇지 않으면 공격당하기 쉬워진다.(hash 함수의 특성)
• 이를 통해 만든 해쉬값 $h$ 를 암호화해서 Signature $S$ 를 만든다.
• 수신자(Alice)는 검증의 과정을 거쳐서 해당 signature 가 valid 한지 판별한다.

Attacks and Forgeries

이러한 Digital Signature 를 공격하거나 위조하는데 어떤 것들이 있는지 살펴보자.

• Key-only Attack
  • A 의 public key 만 알 경우(A 의 signature 가 공격당하는 상황)
• Known message attack
  • message 와 signature 집합에 접근이 가능한 경우
• Generic chosen message attack
  • 공격 전 A 의 public key 와 독립적으로 메세지 리스트를 고를 수 있다.
  • 그리고 A 로부터 고른 메세지의 valid signature 를 얻는다.
• Directed chosen message attack
  • A 의 public key 를 알고 메세지 리스트를 고른다.
  • 그리고 메세지의 valid signature 를 얻는다.

• Adaptive chosen message attack

  • A 를 orcale 로써 사용한다.
  • A 는 이전에 얻은 message-signature pair 에 의존적인 메세지의 signature 를 요청하게 된다.
  • 이는 public key 를 몇 개 얻은 후, 그 다음 것을 고르는 방식이다.
• Break success levels
  1. Total break
     • A 의 private key 를 결정짓는다.
     • 매우 어려운 단계이다.
  2. Universal forgery
     • 해당 algorithm 에 대한 공격이다.
     • 해당 algorithm 과 동등한 signature 를 만들어내는 효율적인 signing algorithm 을 찾는다.
  3. Selective forgery
     • 선택한 하나의 메세지에 대해서만 하나의 페어를 찾아낸다.
     • weak collision hash
  4. Existential forgery
     • 적어도 하나의 signature 를 위조하는 것
     • 전체적인 메세지에 대한 컨트롤은 없다.
     • strong collision hash

Digital Signatures Requirements

이처럼 다양한 공격의 가능성이 있으므로 Digital Signature 는 다음과 같은 requirements 가 있다.

• must depend on the message signed
• unique information 을 sender 에게 사용해야 한다.
  • 이는 양쪽이 위조되고 거부되는 것을 막기 위함이다.
  • unique 하지 않을 경우 더이상 보안이 보장되지 않는다.
• 상대적으로 생산하기(produce) 쉬워야 한다.
• 상대적으로 인식하고 검증하기 쉬워야 한다.
• 위조하는데는 computationally infeasible 해야 한다.
  • 새로운 메세지에 대해 기존의 digital signature 가 이를 만족해야 함.
  • 또한 주어진 메세지의 의심스러운 digital signature 에 대해서도 가능해야 함.
• storage 에 현실적으로 저장 가능해야 함.
  • digital signature 가 비정상적으로 클 경우 storage 에 overhead 가 될 수 있다.

Direct Digital Signatures

Direct Digital Signature 는 이름 그대로 direct 하기에 오직 sender 와 receiver 만 관여한다.

그 내용을 간략히 설명하면 다음과 같다.

• receiver 가 sender 의 public key 를 가지고 있다고 가정한다.
• sender 에 의해 만들어진 digital signature 로 전체 메세지를 sigining 하거나 private key 를 이용해 hash 한다.
• confidentiality 를 위해 receiver 의 public key 를 이용해 암호화 할 수 있다.
• sign 을 먼저 하고 암호화를 진행하고 signature 로 분쟁(dispute)를 다룬다.
• sender 의 private key 에 security 를 의존한다.

ElGamal Digital Signatures

이제 ElGamal Digital Signatures 를 알아보자.

이는 signature 의 변형 중 ElGamal 을 이용한 것으로,

• Galois field 에서 exponentiation 을 사용
• 보안성이 Diffie-Hellman 의 discrete logarithms 계산 복잡성에 의존함

이러한 두 가지 특성을 가진다.

private key 를 이용해 encryption 해서 signing 과정을 진행하고, public key 를 이용해 decrytion 해 verification 과정을 진행한다.

이 때, 각 유저들은 그들의 키를 생성한다.

• 비밀 키를 고른다. $1 \lt x_A \lt q-1$
• public key 를 계산한다.
  • {a, q, and $y_A = a^{x_A} \mod q$}
  • 여기서 a 는 q 의 primitive root 이다.
    이는 앞서 본 ElGamal cryptography 와 유사하다.

signed message M 은 다음과 같이 만들어진다.

1. $m = H(M),\ 0 \leq m \leq (q-1)$ 가 되도록 M 을 hash 한다.
2. $1 \leq K \leq (q-1)$ 인 random integer $K$ 를 고른다. 이 때, $\gcd(K, q-1) = 1$ 이다.
3. temporary key $S_1 = a^K \mod q$ 를 계산한다.
4. $K^{-1} \mod(q-1)$ 을 계산한다.
5. $S_2 = K^{-1}(m - x_AS_1) \mod(q-1)$ 을 계산한다.
6. $(S_1,\ S_2)$ 가 signature 가 된다.

이렇게 만들어진 signed message M 은 user B(any) 가 다음의 과정을 거쳐서 verify 할 수 있다.

• $V_1 = a^m \mod{q}$
• $V_2 = y_A^{S_1}S_1^{S_2}\mod{q}$
• $V_1 = V_2$ 일 경우 valid 한 signature 이다.

이를 증명해보면 다음과 같다.

\[\begin{aligned} V_2 &= y_A^{S_1}S_1^{S_2} \mod{q} \\ &= a^{x_AS_1}a^{KS_2} \mod{q} \\ &= a^{x_AS_1}a^{K\left(K^{-1}\left(m-x_AS_1\right)\right)} \mod{q} \\ &= a^{x_AS_1}a^{\left(m - x_AS_1 \right)} \mod{q} \\ &= a^m \mod{q} \\ &= V_1 \end{aligned}\]

이제 간단한 예제로 ElGamal Signature 를 살펴보자.

• GF(19) 에서 q=19, a=10 일 때, 원시근(primitive root)은 {2, 3, 10, 13, 14, 15}
• A 가 key 를 계산
  • $x_A = 16$ 이라고 했을 떄, $y_A = 10^{16} \mod{19} = 4$
• A 가 message 를 hash $m = 14$ 로 sign
  • random K = 5 라고 하면 gcd(18, 5) = 1
  • $S_1 = 10^5 \mod{19} = 3$
  • $K^{-1} \mod{(q-1)} = 5^{-1} \mod{18} = 11$
  • $S_2 = 11\left( 14 - 16 \cdot 3 \right) \mod{18} = 4$
  • signature = (3, 4)
• B 가 verify 할 때는
  • $V_1 = 10^{14} \mod{19} = 16$
  • $V_2 = 4^3 \cdot 3^4 \mod{19} = 5184 \mod{19} \equiv 16 \mod{19}$
  • 16 = 16 이므로 signature 가 valid 하다.

Schnorr Digital Signatures

이제 Schnorr Digital Signature 에 대해 알아보자.

이 방식 역시 ElGamal Digital Signature 처럼 Galois field 에서 exponentiation 을 활용하는 방식이다.
이는 security 가 DH 의 discrete logarithm 에 의존한다는 의미다.

이 방식의 특징은 message dependent computation 을 최소화한다는 것이다.

• 주요 작업은 메세지에 의존적이지 않고 idle time 안에 완료될 수 있다.
• Message dependent part 는 2n-bit 정수를 b-bit 정수와 곱해야한다.

이 때, prime modulus p 를 이용하게 되는데, p-1 은 q 라는 적절한 size 의 prime factor(소인수) 를 가진다.

• 보통 p 는 1024-bit, q 는 160-bit 정도가 된다.

이러한 p, q 를 잘 설정해야 한다.

Schnorr Key Setup

$a^q = 1 \mod{p}$ 를 만족하는 $a$ 를 고르게 되는데, (a, p, q) 가 global public parameters 가 된다.

각 유저들은 키를 생성하게 된다.

• 비밀 키 $s$ 는 $0 \lt s \lt q$ 를 만족한다.
• public key 는 $v = a^{-s} \mod{p}$ 로 계산한다.

이제 Schnorr Signature 의 과정을 보자.

유저는 message M 을 다음과 같이 signing 한다.

1. random $r$ ($0 \lt r \lt q$) 을 고르고 $x = a^r \mod{p}$ 를 계산

2. message M 을 x 와 합치고 hash 한다. $e = H\left( M\

   \ x \right)$

3. $y = \left( r + se \right) \mod{q}$
4. signature = (e, y)

다른 유저가 verify 하는 과정은 다음을 따른다.

1. $x’ = a^yv^e \mod{p}$

2. $e = H\left( M\

   \ x’ \right)$ 를 계산한다.

위의 과정을 증명해보자.

\[\begin{aligned} x' &= a^yv^e \mod{p} \\ &= a^ya^{-se} \mod{p} \\ &= a^{y-se} \mod{p} \\ &= a^r \mod{p} \\ &= x \mod{p} \\ \text{hence, }&\ H(M\ ||\ x') = H(M\ ||\ x) \end{aligned}\]

Digital Signature Standard(DSS)

Digital Signature Standard 는 NIST & NSA 에서 90년대 초반 고안했다.

이는 SHA hash algorithm 을 이용하며 DSA 를 표현한다.DSS 는 표준이고 DSA 는 알고리즘이다.

1991년 FIPS-186에서 publish 되었으며 93, 96, 00년에 개정되었다.

2000년 FIPS 186-2 에서 RSA 와 Elliptic curve cryptography 기반의 DSA 가 포함되었다.

RSA 와는 달리 DSA 는 암호화나 키 교환에 사용될 수는 없다.

여기서 ECC 는 resource limited 한 곳에 사용된다.(특성상 효율적)

그리고 DSA 는 not reversible 하다.

DSS vs RSA Signatures

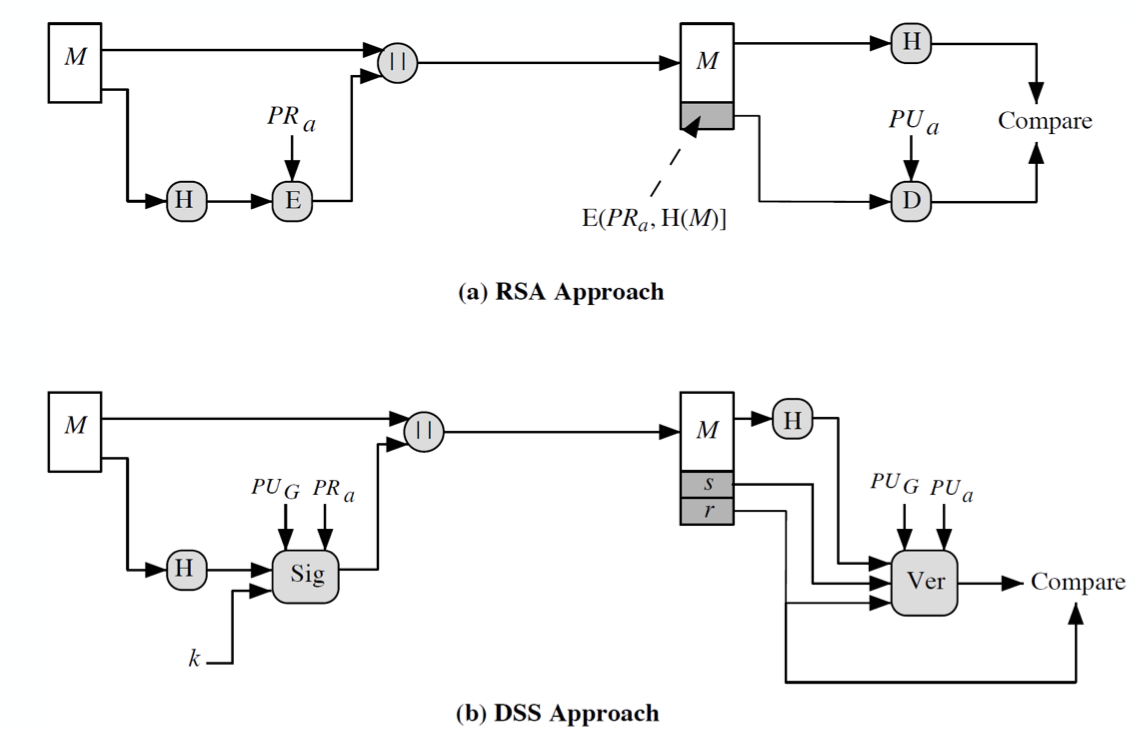
RSA 방식과 DSS 방식의 구조적 차이점을 다음과 같이 확인할 수 있다.

Digital Signature Algorithm(DSA)

DSA 는 320-bit signature 를 512~1024-bit security 로부터 생성한다.
이는 RSA 보다 작으면서도 빠른 것이다.

• 320 vs. 1024 bits, modulo 160-bit

그러나 이는 digital signature scheme 만 할 뿐 암호화나 키 교환을 위해서 사용되지는 않는다. 이 역시 앞서 나왔던 것들처럼 discrete logarithm 의 계산 복잡성에 보안성을 의존한다.

구조를 잘 살펴보면 ElGamal 과 Schnorr scheme 의 변형임을 확인할 수 있다.

DSA Key Generation

DSA 는 global public key value (p, q, g) 를 가진다.

• prime $q$ 는 160-bit 이다.
• large prime $p,\ 2^{L-1} \lt p \lt 2^L$ 를 고른다.
  • L = 512~1024 bits 를 가진다. 이 때 64의 배수형태를 띄도록 한다.
  • $q$ 는 ($p-1$) 의 prime factor(divisor) 이다.
• $g = h^{\left( p-1 \right) \over q}$ 인 $g$ 를 고른다.
  • $1 \lt h \lt p-1$ 이고 $h^{\left( p-1 \right) \over q} \mod{p} \gt 1$ 이어야 한다.

이제 private key 를 고르고 public key 를 계산한다.

• choose random private key $x \lt q$
• compute public key $y = g^x \mod{p}$

DSA Signature Creation

message M 을 어떻게 signing 하는지 알아보자.

1. random signature key $k,\ k \lt q$ 를 생성한다.

   • 이 때 $k$ 는 반드시 random 이어야하며 사용하고나면 재사용하지 않고 destroy 해야 한다. 재사용할 경우 보안성이 깨질 수 있다.

2. signature pair 를 계산한다.

   • $r = (g^k \mod{p}) \mod{q}$
   • $s = \left[k^{-1}\left(H\left(M\right) + xr\right)\right] \mod{q}$

이렇게 구한 signature pair(r, s) 를 메세지 M 과 같이 보낸다.

DSA Signature Verification

DSA Signature 를 verify 하는 과정을 살펴보자.

\[\begin{aligned} x &= s^{-1} \mod {q} \\ u_1 &= [H(M)w] \mod{q} \\ u_2 &= (rw) \mod{q} \\ v &= [(g^{u_1}y^{u_2}) \mod{p}] \mod{q} \end{aligned}\]

이 때 $v = r$ 이면 valid 하다.

위의 과정을 증명해보자.

\[\begin{aligned} s &= [k^{-1}(H(M) + xr)] \mod{q} \\ \text{thus, } k &\equiv H(M)s^{-1} + xrs^{-1} \\ &\equiv H(M)w + xrw \mod{q} \\ \end{aligned}\]

Since $g$ has order $q \mod{p}$, we have

\[\begin{aligned} g^k &\equiv g^{H(M)w}g^{xrw} \\ &\equiv g^{H(M)w}y^{rw} \\ &\equiv g^{u_1}y^{u_2} \mod{p} \end{aligned}\]

DSS Overview

위의 과정을 도식으로 보면 다음과 같다.

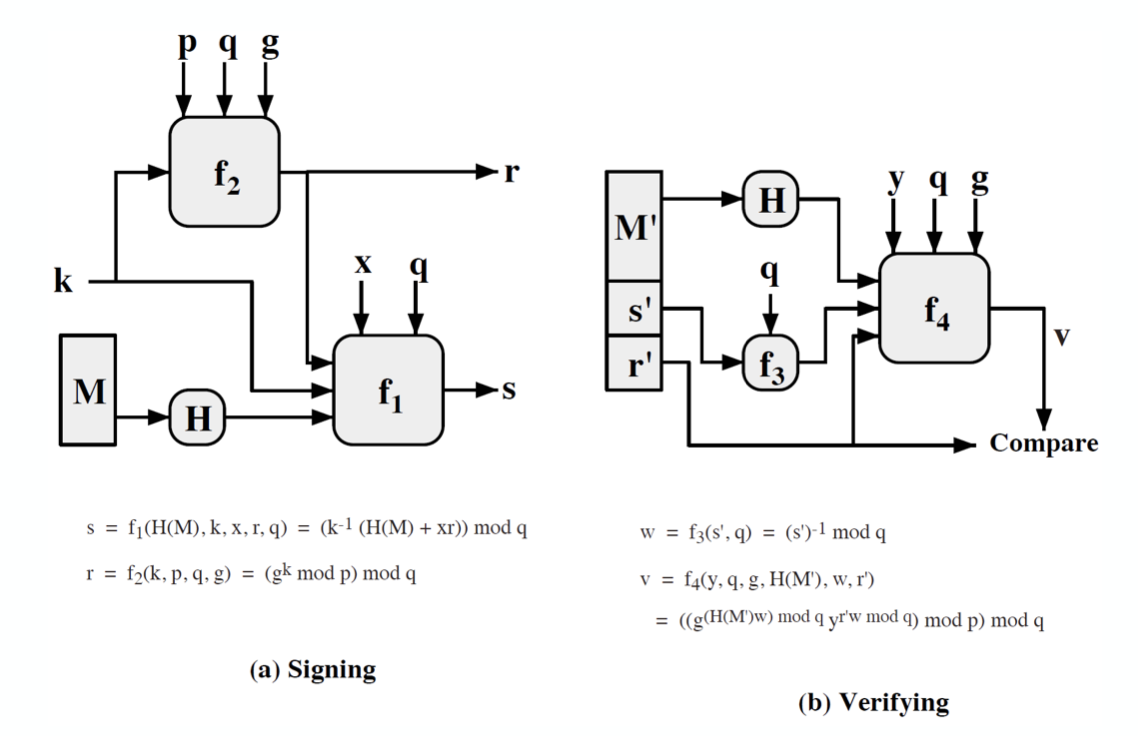
이 때 메세지에 의존적이지 않은 $r$ 에 대한 마지막 테스트를 하게 된다.Compare 연산인듯 하다

계산이 많이 필요한 부분은 exponential calculation 인 $g^k \mod{p}$ 와 $k^{-1}$ 이다.

• sign 될 메세지에 의존적이지 않기 때문에 $r$ 과 $k^{-1}$ 을 미리 계산할 수 있다.

Public Key Certificate

누군가의 public key 를 다른 이에게 전달하기 위해서는 어떻게 해야할까?

• broadcast 를 한다.
• 편리하지만 누구나 이 announcement(broadcast) 를 위조하기 쉽다.

이러한 물음에 답하기 위해 public key certificate 를 고안하게 되었다.

• public key + ID of the key owner 로 구성된다.
• 전체 block 이 신뢰하는 third party, certificate authority(CA) 로부터 sign 된다. (RSA, DSA 사용)

이와 관련하여 X.509 가 universally 하게 accept 된 public-key certificate 이다.(IPsec, TLS, SSH, S/MIME, …)

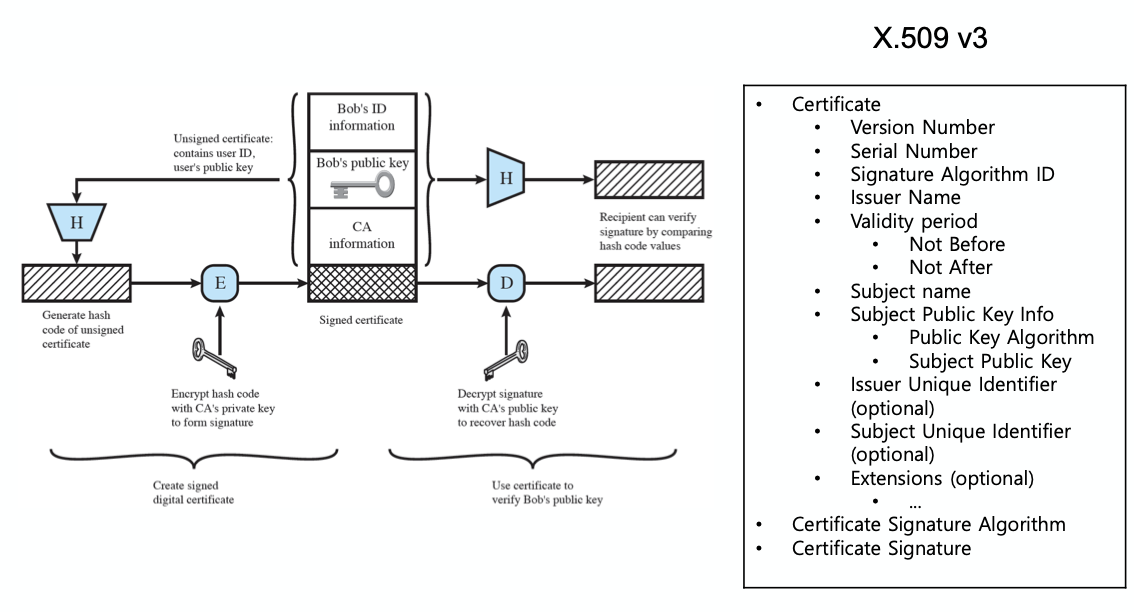
여기서 CA 는 모든 시스템으로부터 완전히 신뢰된 것이다.
이런 신뢰의 문제는 사실 계속 꼬리를 물 수 밖에 없기 때문에 이렇게 공인된 존재가 필요하게 된다.

Group Signature

Group Signature 는 Eurocrypt 에서 91년도에 D.Chaum 이 발표한 것으로 그룹에 속한 멤버가 익명으로 signing 을 진행하게 된다.

이렇게 만들어진 signature 는 어떤 그룹이 서명한 것인지는 알 수 있으나 어떤 유저가 서명했는지는 알기 어렵게 되는 이점이 있다.
즉, anonymity 가 지켜진다.

그러나 group manager 가 있고 이 group manager 는 누가 signing 을 했는지 알 수 있다.

Group Signature 의 특징은 다음과 같다.

• Unforgeability
  • 그룹의 멤버만이 메세지를 정확하게 sign 할 수 있다.
• Anonymity/Traceability
  • 그룹 멤버 중 누가 서명했는지 알 수 없지만 그룹 매니저는 이를 추적할 수 있다.
• Unlinkability
  • 같은 그룹내의 멤버가 두 signature 를 발행(issue)했는지 결정할 수 없다.
• Security against framing attack
  • 어떤 그룹 멤버가 다른 멤버를 위해 대신 signing 할 수는 없다.

Ring Signature

Ring Signature 는 Group Signature 의 변형 중 하나이다.

• 개별 signature 의 anonymity 를 revoke 할 방법이 없다.
• 어떤 그룹의 유저든간에 추가 설정 없이 그룹으로 사용될 수 있다.

Application to Cryptocurrency

이러한 Ring Signature 를 활용해 암호화폐를 구현한 것이 Monero 이다.

Monero 의 특징은 다음과 같다.

• transaction 간의 linkage 를 숨긴다.(unlinkability, untraceablility)
• Ring signature 가 유저의 account key 를 사용하고 public key 들이 blockchain 으로부터 pull 된다.
• 가능한 signer 들이 ‘ring’ 안에서는 모두 동등하고 valid 하다고 본다.
• 외부자(outsider)가 유저의 account 안에 어떤 signer 가 있는지 말할 수 없다.
• 이로 인해 transaction 이 untraceable 하게 된다.

최종 수정일 : 2019-12-10

본 포스트는 학부-_정보보호_ 를 공부하며 정리한 글 입니다.
잘못된 내용이 있다면 알려주세요!
감사합니다 :)